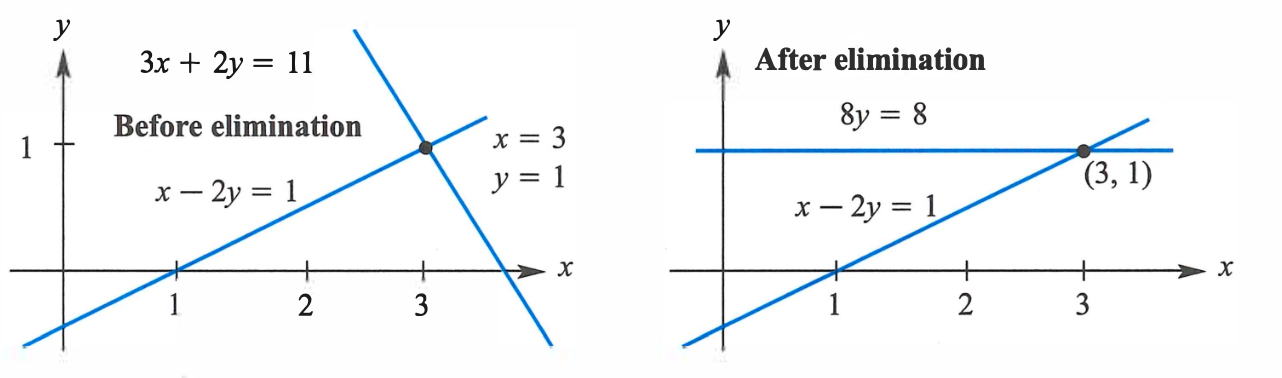向量与方程
考虑如下线性方程组所示的线性系统:
逐行观察,则两方程分别在「行图」(row picture)—— 平面生成一条直线,其交点 为方程组的解。
列图(column picture)则从向量的视角解读:
解方程组的问题变为确定左侧向量的线性组合,使之生成右侧向量 。此处 ,,其列图如下
以矩阵形式改写,记上述方程组左侧的 系数矩阵(coefficient matrix)为 ,得到矩阵方程 :
分别分析矩阵的行向量组和列向量组得到的行图和列图均代表相同的线性方程组。对于形如上述未知数个数与方程个数相同的线性系统,通常存在一个解。而含两个方程和三个未知数的线性方程组的解通常构成一条直线。据此易将概念推广至更高维度。例如,对于 矩阵,其行图中,每个方程(每行)对应三维空间中的一个平面,三个平面通常交于一点(原点);列图中,三个列向量的线性组合生成向量 。
回顾矩阵
我们将矩阵内的元素记为 ,其中 给出元素位置的行标, 给出列标,即 是位置 的元素,计算软件中也将其表示为 。
对于 矩阵 ,其中共有 个元素,可表示为 。其构成的矩阵方程可表示为
即,
从行形式看, 的第 个分量为
其中,
也就是说, 行 列矩阵 左乘含有 个分量的向量,结果为含有 个分量的向量。所构成的线性方程组含有 个方程,这些方程所对应的平面在 维空间中,其列向量的线性组合 在 维空间中。
消元
消元(elimination)是一种解线性方程组的系统性方法,其过程产生三角系统(triangular system),然后对三角系统应用回代(back substitution)即可逐步求解。消元的基本运算是从一个方程减去另一方程的倍数,系统由于未知数的减少而变为三角形。
我们设定目标为得到能自下而上求解的上三角形系统。乘数(multiplier),记为 ,为待消项系数除以主元(pivot)——用于消元的行的第一个非零系数。主元位于消元所得三角形系数矩阵的对角线上。求解 个方程需要 个主元。
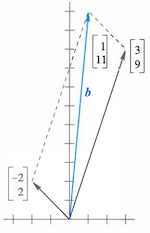
例如,
回代 即解得 。若还有第三个方程,则可继续利用消元所得到新的第二个方程消去 。注意到,消元前后的方程组拥有相同的解,如图所示。
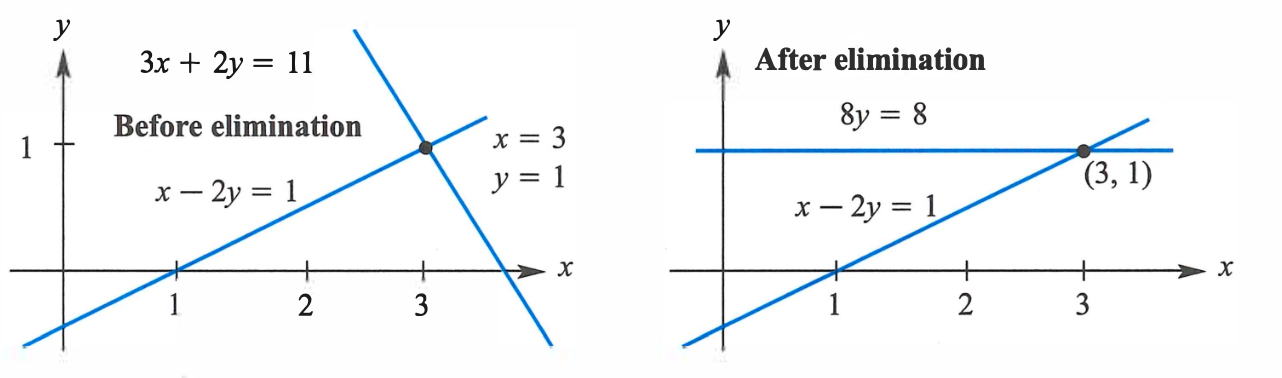
主元在消元过程中被用作除数,因而不能为 。此时需要调整方程顺序。例如,对于第一个主元位的数为 的情况:
交换方程得到
上述情形均存在完整主元集(full set of pivots),故存在唯一解且能应用消元法。我们称缺少主元的线性系统奇异(singular),此时使用消元法将中止:或得到 ,方程组无解;或得到 ,方程组有无穷多解。例如,
尝试消元得到
显然,从行图看,两行所构成的直线平行而不相交;从列图看,两列向量共线,故其所生成的向量在直线上。又如,
尝试消元得到
由于两方程相同, 可任意取值,而 的值与之相关。此时行图中仅存在一条直线——方程组有无穷多解。
从 到
上述向下消元之流程适用于一般的 方程组,且我们仅需关注系数矩阵 的变化:使原方程组 逐列转变为上三角形(upper triangular)方程组 。例如,对于 方程组的系数矩阵,消元后最终应得到
之形式,其中的字母代表 原方程各分量系数。对于第三列之后的列,消元过程可能需要重复执行。记乘数 为第 行待消项系数除以第 行主元之系数,则每当从第 个方程中减去第 个方程的 倍,系数矩阵中的 元素被设为 。即,使用 消元后, 元素被设为 。
矩阵形式
考虑矩阵形式的线性方程组 :
其解向量 。分析利用上述消元法解该线性方程组之过程,第一步为从第二个方程减去第一个方程的 倍,故 的第二分量需减去第一分量的 倍。要达成这样仅改变列向量中一个分量,而其他分量不变的效果,我们使用由单位矩阵 中的一个 替换为乘数 的「初等矩阵」(elementary matrix)。例如,
上述过程的逆过程(inverse)为将第一个方程的 倍加到第二个方程,故 的逆矩阵 可表示为
初等矩阵 主对角线上的元素为 ,第 行第 列,即 上则为非零元素 。 左乘向量即从其第 行减去第 行的 倍。
我们的目标是使用适当的矩阵 同时左乘方程等号两侧,即 。因此,还需考虑方程左侧的 。向量 应保持不变,仅系数矩阵 变化。事实上,新系数矩阵 是 左乘 的结果,而上述表达式的变化规律恰好符合此目标。
我们以此消元问题尝试分析两个一般矩阵相乘,即 的结果:
通常来说,对矩阵乘法,结合律(associative law)成立,即 ;而交换律不成立,即 。事实上,对于前述矩阵, 表示 右乘 ,其作用于 的列,而不是行,结果为从 的第一列减去第二列的两倍:
若矩阵 仅有一列,则矩阵乘法运算律与矩阵-向量运算律保持一致,此规则也适用于对上述矩阵乘法的逐列分析: 的第一列正是 左乘 的第一列:
总之,矩阵乘以列向量的结果为列向量,我们已通过几何背景理解这一事实。为理解更复杂的矩阵乘法运算,需要记住事实上,行向量乘以矩阵的结果为行向量,其运算过程相似。例如,
置换矩阵(permutation matrix) 表示用于置换矩阵元素位置的矩阵。换行矩阵用于主元位置元素为 ,而其下方为非零元素时需交换两行以继续消元的情况。换行矩阵的构造同样基于单位矩阵,仅需将其 两行交换。例如,
由于消元法本质上对系数矩阵 和常数项向量 进行相同的行变换,通常将 引入系数矩阵同步消元,以 这一列扩展后矩阵 称为增广矩阵(augmented matrix),记作 。
消元法作用于增广矩阵的整行:
上述矩阵乘法中, 作用于增广矩阵。分别从行或列的视角看待得到相同的结果。此外,也可以按元素(entry)计算。例如,上述结果矩阵中 上的 可视作经左侧矩阵第 行与右侧矩阵第 列计算得到。考虑矩阵乘法
按前述方法依次用 的行左乘 的列——其本质为向量的点积运算,便可得到结果矩阵中的各个元素。例如,
另一种非常规的方法是分别以 的列左乘 的行得到矩阵,最终相加。
矩阵运算
根据向量运算的几何背景,矩阵能与任意常数 相乘,同型矩阵可相加:
矩阵 是 与 相乘的结果, 与 相加得到零矩阵 。多数运算律适用于矩阵运算,而如前所述,仅需注意交换律不适用于矩阵乘法,即 ,例外为对与方阵 同阶的单位矩阵 有 ,故仅有 与同阶方阵相乘可交换。
根据矩阵乘法结合律,方阵的幂,记为 ,遵守与数字幂相似的法则,因此有
矩阵乘法
,即 左乘 有意义的前提为,若 有 列,则 须有 行,方能确保可用 左乘 的每列。例如,若 和 均为 矩阵,则 无意义。要使其有意义, 应当为 矩阵。
设 为 矩阵, 为 矩阵,则 为 矩阵。一行( 矩阵)左乘一列( 矩阵)的结果为 矩阵,其中的值即为两向量点积。事实上,对于任意矩阵 、,其乘积 完全由点积构成。因此,计算矩阵乘法 的一种方法是计算 中每一行与 中每一列的点积。记 中第 行第 列的元素为 ,则
的第行的第列
特别地,若 和 均为 阶方阵,则 也为 阶方阵,其中包含 个点积。每个点积由 次乘法运算得到,故计算 需要 次乘法运算。
左乘各列/各行左乘
整体来看, 左乘 的各列分别得到其在 中对应位置的列,换言之, 的各列即为 的列向量的线性组合。即,矩阵乘法的列图可表示为
与之相反, 各行左乘矩阵 得到其在 对应位置的行。换言之, 的各行为 的所有行向量的线性组合。矩阵乘法的行图表示为
上述行-列图视角可用于计算矩阵乘法,但其本质仍为点积计算。计算 可简记为
其中每个点积由 次乘法计算、 次加法计算得到,故矩阵乘法共含 次乘法运算、 次加法运算。
列左乘行之和
考虑以下二阶方阵乘法,使用上述三种方法任意一种可得
注意到,上式可拆分为两个部分:
即矩阵乘法 等于其第一列左乘第一行与第二列左乘第二行之和。上述「列左乘行」的矩阵乘法计算方法适用于一般情形。对于 矩阵 、 矩阵 , 有 列, 有 行,故对于 ,将分别用 的第 列左乘 的第 行所得的共计 个 矩阵相加即为 。
分块矩阵
我们可以将矩阵按需要分割为子块(blocks)。例如,增广矩阵 便含两个形状不同的子块。若矩阵 中子块与矩阵 中子块均能应用矩阵乘法,即 中列的分割与 中行的分割相对应,则允许使用子块乘法计算 。例如,考虑如下包含四个子块的矩阵
对常规矩阵消元利用了乘数 。类似地,对于上述含子块的矩阵,若 可逆,则能利用含 的矩阵 消元:
注意到,此处 替代了常规矩阵消元中 ,单位矩阵 替代了乘法单位元 。最后的子块 如同 ,称为舒尔补(Schur’s complement)。